Once we lift our sack of potatoes into the air, we will have potential energy. You can think of an analogy as the water in a reservoir behind a hydropower dam. The stored energy in the reservoir is converted into kinetic energy (motion) as the water flows down a large pipe and spins a turbine.
First, let’s calculate how much work (here, energy measured in lb*ftf and joules) is needed to lift a 5-lb sack of potatoes 5 ft in the air.
- 5 lbm weighs 5 lbf (5 lbmass weighs 5 lbforce) [1]
- Work = Force * Distance [2]
- Work = (5.0 lbf) * (5.0 ft) = 25 ft*lbf [3]
Let’s make the SI conversion. We will use a few conversion factors to accomplish this task.
First, let’s convert lbm to kg (the SI unit for mass):
- 5.0 lbm * 0.454 kg/lbm = 2.3 kg [4]
Next, let’s convert ft to m (the SI unit for length):
- 5.0 ft * 0.3048m/ft = 1.5 m [5]
And then, we want to get a number for force that is in SI units of Newtons – we need to make our force calculation using our SI unit of kg and the gravitational acceleration constant of 9.8 m/s2:
- F = ma (mass * acceleration) = 2.3 kg * 9.8 m/s2 = 23 N [6]
Lastly, to calculate the energy or work, we must multiply the force (N) through the distance lifted (m) in this case:
- Work = (23 N) * (1.5 m) = 34 J [7]
Releasing the potential energy
We store the energy when we lift the weight, but how can we “release” the energy? We drop the potatoes. We know that one drop equals 25 ft*lbf [3] or 34 J [7] from our previous calculations. But we originally calculated the energy for our hot shower in BTUs. Thus, we must do another conversion. (By the way, engineers are always doing conversions, because they are often doing work between different systems with different conventions.)
Let’s start by converting 25 ft*lbf in [3] above to BTUs. This conversion will allow us to calculate how many cycles are required, picking up the 5-lb sack of potatoes 5 ft in the air and dropping the sack of potatoes, to produce a single BTU of energy.
\[\begin{array} 1\ \text{Btu} =778\ \text{ft} \cdot \text{lb}_{\text{f} }\\\\ \displaystyle\frac{25\ \text{ft} \cdot \text{lb}_{\text{f} } }{\text{cycle} } \times \frac{1\ \text{Btu} }{778\ \text{ft} \cdot \text{lb}_{\text{f} } } =0.03\frac{\text{Btu} }{\text{cycle} } \\ \displaystyle\frac{1}{\frac{0.03\ \text{Btu} }{\text{cycle} } } =31\frac{\text{cycles} }{\text{Btu} } \end{array}\]
Therefore, 31 ‘potato’ cycles are required to produce enough energy equal to a single BTU.
Using Human Power
For this next step you will need a timer and your 5lb sack of potatoes. Energy equals work, but power equals work per unit of time.
Energy → BTU
Power → BTU/min
Let’s see if we can generate enough power to produce 1 BTU per minute. Can you complete 31 cycles in 60 seconds? Try it out now!
\[\frac{31\ \text{cycles} }{\text{minute} } \times \frac{1\ \text{Btu} }{31\ \text{cycles} } =1\ \frac{\text{Btu} }{\text{minute} } \quad \Leftarrow \text{Power} \]
Thinking back to our shower, how long must our human generated power plant work to supply enough energy for our hot shower? If energy divided by power equals time, how much time will it take if the energy required is 40,000 BTU and the power available is 1 BTU/minute? Once you calculate the necessary minutes, convert your answer into days. Check your answer below.
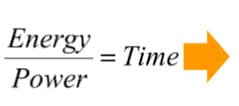
Equation One: 40,000 BTU / 1 BTU per minute = __________ minutes
Equation Two: _________ min * (1 hr/60 min) * (1 day/24 hr) = ____________ days
If our power plant consisted of one person supplying our energy by picking up and dropping a 5-lb sack of potatoes, it would take 28 days just to supply enough energy for one hot 20-minute shower. However, in modern society the energy we demand is delivered in real time, as we need it.
